Introduction: Searching for Clarity in the Fog
Imagine walking through a thick fog, trying to map the path ahead. You can see vague outlines trees, lampposts, maybe even a sign but not enough to know where you truly are. This is what data scientists face when working with datasets that have hidden or latent variables. The Expectation–Maximisation (EM) algorithm is the lantern that gradually illuminates this fog, step by step, helping us estimate what we cannot see directly.
In the landscape of statistical modelling, EM acts like a patient explorer iterating between guessing what’s hidden and refining those guesses until the unseen structure of data becomes clear. This technique powers many modern tools, especially those you’ll encounter in an Artificial Intelligence course in Delhi, from speech recognition systems to image clustering applications.
The Story Behind the Algorithm: Two Steps to Convergence
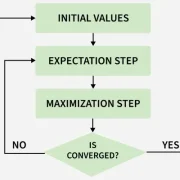
The EM algorithm is built on an elegant idea: alternate between estimating what’s missing and optimizing the model based on those estimates.
It begins with an initial assumption about the model parameters. In the Expectation (E) step, the algorithm imagines or “expects” the values of the hidden variables based on the current parameter estimates. It’s a bit like trying to fill in missing jigsaw pieces by predicting their shape from the surrounding ones.
Then comes the Maximization (M) step the model recalibrates itself, updating the parameters to maximize the likelihood of the data given those newly estimated hidden values. The two steps repeat in a loop: guess, optimize, refine, repeat. Over time, the estimates settle into stability a point known as convergence, where the likelihood stops changing significantly.
It’s this cyclical dance that gives EM its enduring beauty and power a self-correcting mechanism that learns from its own predictions.
The Hidden World of Latent Variables
Latent variables are the “ghosts” of data analysis invisible but influential. They represent aspects of the data we cannot directly measure but that shape observable patterns.
Consider a marketing example: customers may exhibit similar purchasing behaviours not because they share demographics but due to unobserved traits like brand loyalty or risk tolerance. These hidden factors are latent variables. EM helps reveal them, allowing data scientists to model reality more faithfully.
In Gaussian Mixture Models (GMMs), one of EM’s most celebrated applications, these hidden variables correspond to the probability that a given data point belongs to a specific Gaussian distribution. Through iteration, EM refines both the shape of these distributions and the assignments of points turning an initially chaotic dataset into neatly separated clusters.
Such mastery over uncertainty is precisely what students aim to acquire through an Artificial Intelligence course in Delhi, where they learn not only to handle visible data but also to model the unseen forces driving it.
Why EM Matters: From Genes to Galaxies
The reach of EM extends far beyond textbooks and labs. It is a quiet workhorse in a range of scientific and commercial fields.
In genetics, EM helps in estimating haplotype frequencies where researchers must infer missing data about genetic sequences. In computer vision, it powers image segmentation, allowing systems to distinguish between overlapping or obscured objects. In finance, it’s used for credit risk modelling, where not all influencing factors are directly measurable.
Even in natural language processing, EM assists algorithms in tasks such as topic modelling, helping uncover the hidden themes that bind documents together. Whether it’s DNA strands, market behaviours, or textual nuances, EM provides a unifying framework to extract meaning from incomplete information.
The Challenges Beneath the Elegance
Yet, EM is not without its trials. Like a hiker choosing a trail in fog, it can converge to a local rather than global optimum meaning the algorithm may settle for a “good enough” solution that isn’t truly the best. Its performance also depends heavily on the initial guess of parameters; a poor start can lead to misleading results.
Moreover, EM can be computationally expensive for large datasets. Since it iterates until convergence, each loop can consume significant processing power. Researchers often refine it through variations like Stochastic EM or Variational EM, which balance accuracy with speed.
Despite these challenges, EM’s conceptual simplicity and versatility make it one of the most dependable techniques in statistical inference the mathematical equivalent of learning from partial truths.
A Metaphor for Learning Itself
Think of EM as how humans learn from uncertainty. When faced with incomplete information, we make an assumption, act upon it, observe the outcomes, and then refine our belief. Whether it’s learning to play an instrument or understanding another person’s emotions, we oscillate between expectation and adjustment.
In that sense, EM mirrors the very process of cognition making it a profoundly human algorithm. It demonstrates that learning isn’t always about having all the answers at once, but about improving through iteration and reflection.
Conclusion: The Art of Revealing the Invisible
The Expectation–Maximization algorithm stands as a cornerstone of modern statistical learning, embodying both mathematical rigour and philosophical depth. It reminds us that insight often emerges not from seeing everything at once, but from illuminating what’s hidden, one layer at a time.
In the evolving world of data science, where uncertainty and incompleteness are constants, EM remains an invaluable companion a steady guide through the fog of unknowns. For anyone pursuing an Artificial Intelligence course in Delhi, mastering EM isn’t just about solving equations; it’s about embracing the mindset of iteration, discovery, and refinement the essence of intelligent learning itself.








Comments